
이번 글을 통해 배워갈 내용
- 백준 문제 2407번 풀어보기
- 조합의 정의
- 조합을 C++로 풀어보기 (비효율적 방법)
- 조합을 C++로 풀어보기 (memoization, pascal 삼각형)
자 그럼 백준 문제 nCr 조합구하기를 풀어보겠습니다.
10분 정도 풀어보시고 해답이 안나오신다면 아래 글을 보시고 풀어보시면 됩니다.
https://www.acmicpc.net/problem/2407
2407번: 조합
n과 m이 주어진다. (5 ≤ n ≤ 100, 5 ≤ m ≤ 100, m ≤ n)
www.acmicpc.net
조합(Combination)의 정의
조합은 서로 다른 n 개의 원소 중에서 순서 상관없이 r 개를 선택하는 경우의 수를 구하는 것입니다.
이는 nCr 로 표현하며
n 은 전체 갯수
r 은 선택된 갯수 입니다.
nCr 은 다음과 같은 공식으로 표현합니다.
n! / ( (r!) * ( (n-r)! ) )
아래의 이미지를 참조하시면 좋습니다.

그렇다면 프로그래밍으로 어떻게 조합을 구할수 있을까요?
아래 코드는 제가 시도한 첫번째 방법입니다.
#include <iostream>
using namespace std;
// 임의의 배열 최대 값
#define MYMAX 200
// factorial memoization 배열 선언
long g_factorialArray [MYMAX];
long findFactorial(int n)
{
if(n<=1)
{
g_factorialArray[n] = 1;
return 1;
}
else
{
if(g_factorialArray [n] != 0)
{
return g_factorialArray [n];
}
else
{
g_factorialArray[n] = findFactorial(n - 1) * n;
return g_factorialArray[n];
}
}
}
long findCombination(int n, int r)
{
long tempDenominator = findFactorial(r) * findFactorial(n-r);
long tempNumerator = findFactorial(n);
return (tempNumerator/tempDenominator);
}
int main()
{
cout<<findCombination(100,100);
return 0;
}
조합을 구할때 위와 같이 풀게 되면 작은 수에 경우 문제 없이 풀수 있지만
int, long, long long 등의 자료 구조상 변수가 담을 수 있는 크기를 가볍게 넘어 버립니다.
예시)
100! = 100 x 99 x 98 x 97 x 96 x 95 x 94 x 93 x 92 x 91 x 90 x 89 x 88 x 87 x 86 x 85 x 84 x 83 x 82 x 81 x 80 x 79 x 78 x 77 x 76 x 75 x 74 x 73 x 72 x 71 x 70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59 x 58 x 57 x 56 x 55 x 54 x 53 x 52 x 51 x 50 x 49 x 48 x 47 x 46 x 45 x 44 x 43 x 42 x 41 x 40 x 39 x 38 x 37 x 36 x 35 x 34 x 33 x 32 x 31 x 30 x 29 x 28 x 27 x 26 x 25 x 24 x 23 x 22 x 21 x 20 x 19 x 18 x 17 x 16 x 15 x 14 x 13 x 12 x 11 x 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1
unsigned long int 범위 0 에서 4,294,967,295까지
그렇다면 어떻게 풀어야 할까요?
스트링 값을 넣어서 풀어야 할까요?
결과 값은 생각보다 작지만 중간에 큰 값이 들어간다면 방법을 바꿔야 할까요?
한가지 확실한 건
기존의 memoization 방법에 무엇인가 새로운 방법을 더해서 풀어야함은 분명합니다.
해답은 파스칼의 삼각형에 있었습니다.
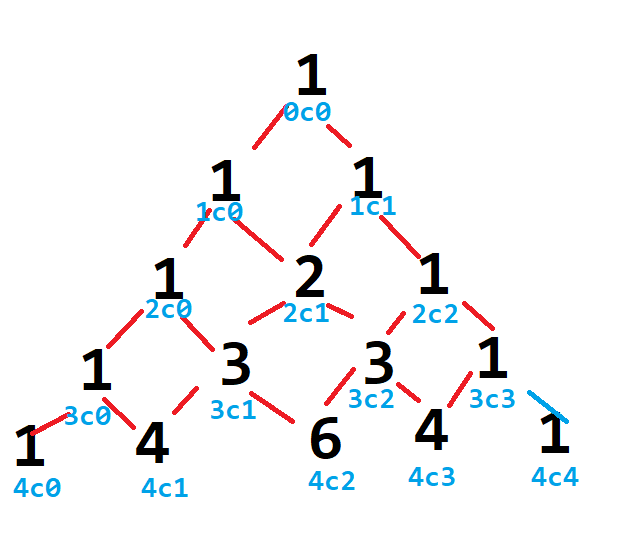
위와 같이 계속 재귀적으로 숫자를 스트링값으로 증가시키면서 memoization으로 중간 값을 저장해주면
100C1 같이 큰 값도 쉽고 빠르게 구현 할수 있습니다.
만약 위에 내용이 이해가 되셨다면 다시한번 10분간 도전해보시고 정 안되실 경우
아래 내용을 읽어 보시길 바랍니다.
스트링으로 두 수를 더하는 부분이 조금 오래 걸렸던 것 같고
재귀적으로 근본을 이해하고 푸니까 쉽게 풀수 있었다
메모아이제이션 기법으로 중간 값을 저장함으로서 속도 향상도 이루어내었다.
#include <iostream>
#include <algorithm>
using namespace std;
// 임의의 배열 최대 값
#define MYMAX 200
// factorial memoization 배열 선언
string g_nCrArray [MYMAX][MYMAX];
string addTwoLargeNumbers(string str1, string str2)
{
if(str1.length()> str2.length())
{
swap(str1, str2);
}
string tempStr = "";
int str1Length = str1.length();
int str2Length = str2.length();
int difLength = str2Length - str1Length;
int carry = 0;
for(int i=(str1Length-1); i>=0; i--)
{
int sum = (str1[i] - '0') + (str2[i+difLength] - '0') + carry;
tempStr.push_back(sum%10 + '0');
carry = sum / 10;
}
for(int i=(difLength - 1); i>=0; i--)
{
int sum = (str2[i] -'0') + carry;
tempStr.push_back(sum%10 + '0');
carry = sum / 10;
}
if(carry)
{
tempStr.push_back(carry+'0');
}
reverse(tempStr.begin(), tempStr.end());
return tempStr;
}
string findCombination(int n, int r)
{
if(n==r || r ==0)
{
g_nCrArray[n][r] = "1";
return "1";
}
if(g_nCrArray[n][r]!="")
{
return g_nCrArray[n][r];
}
else
{
g_nCrArray[n-1][r-1] = findCombination(n-1, r-1);
g_nCrArray[n-1][r] = findCombination(n-1, r);
return addTwoLargeNumbers(g_nCrArray[n-1][r-1], g_nCrArray[n-1][r]);
}
}
int main()
{
int n, m;
cin >> n >> m;
cout<< findCombination(n, m);
return 0;
}결과

뭔가 깔끔하게 해결해서 기분 좋았고
코드를 푸니까 즐거워 지는 하루다.
오늘도 즐거운 코딩하시길 바랍니다 ~ :)
참조 및 인용
https://ko.wikipedia.org/wiki/%EC%A1%B0%ED%95%A9
조합 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 조합론에서 조합(組合, 문화어: 무이, 영어: combination)은 집합에서 서로 다른 n개의 원소 중에서 순서에 상관없이 r개를 선택하는 것이다. 그 경우의 수는 이항계
ko.wikipedia.org
https://stackoverflow.com/questions/11809502/which-is-better-way-to-calculate-ncr
Which is better way to calculate nCr
Approach 1: C(n,r) = n!/(n-r)!r! Approach 2: In the book Combinatorial Algorithms by wilf, i have found this: C(n,r) can be written as C(n-1,r) + C(n-1,r-1). e.g. C(7,4) = C(6,4) + C(6,3) ...
stackoverflow.com
https://stackoverflow.com/questions/10492820/summing-large-numbers
Summing Large Numbers
I have being doing some problems on the Project Euler website and have come across a problem. The Question asks,"Work out the first ten digits of the sum of the following one-hundred 50-digit numbe...
stackoverflow.com
C++ Primer
'C++ > C++ 알고리즘' 카테고리의 다른 글
| 백준 2953번 나는 요리사다 C++로 간단하게 풀기 (1) | 2021.07.01 |
|---|---|
| 백준1914번 하노이 탑(Hanoi tower) C++로 구현해보기 (1) | 2021.06.20 |
| C++과 테일러 급수로 sin(x), cos(x), e^x 값 계산해보기 (1) | 2021.06.19 |
| 등차수열의 합을 C++ 프로그래밍 하는 3가지 방법 (1) | 2021.06.19 |
| 재귀어에게 배우는 쉬운 재귀 (1) | 2021.06.17 |
